| Home |
|
PREFACE | PRIMEVAL | SPECIAL | GENERAL | CONCLUSION |
| Dictionary | Maxwell | Minkowski | Twins | Light Cone |
 What's new
For a new visualization of the Twin Paradox, visit |
Here's how the story runs:
The use of "twins" was just to make the story sound more dramatic. Here is a less-dramatic formulation:
On their twenty-first birthday, Peter leaves his twin Paul behind on earth and goes off in the x direction for seven years of his time (0.22 billion seconds) at (24/25)=0.96 the speed of light, then reverses direction and in another seven years of his time returns at the same speed.
- What is Peter's age at the moment of reunion?
- What is Paul's age at the moment of reunion?
(essentially from Spacetime Physics, ex. 27)
What's going on?
You and I meet. We synchronize our watches, and agree to meet up later (here or at some other designated location). When we meet that second time, we will find that our watches are no longer synchronized.
Your watch measures the lapse of your proper-time My watch measures the lapse of my proper-time.
Recall that "the proper time of an observer" is a private issue; it is the spacetime-length of the path that that particular observer took starting out from the first meeting event and returning to the second meeting event.
(In Einstein-Minkowski space) Given an inertial observer's worldline, the elapsed Proper-time between two events along his worldline is the Interval between those events.
"the Interval between A and b" represents the time-elapsed along the trip from A-to-b. Observe that it is one-half the total time-elapsed on the trip from A-to-b-to-C.
Similarly, "the Interval between A and B" represents the time-elapsed along the trip from A-to-B. Observe that it is one-half the total time-elapsed on the trip from A-to-B-to-C, or simply "A-to-C" since A, B, C lie on a straight line (the path of an inertial observer).
We wish to demonstrate the Twin Non-Paradox by showing that: at the end of the round-trip, the Proper-time elapsed for each observer differs, depending on the nature of their nature of their worldline.
We wish to show explicitly that the total Proper-time elapsed for the A-B-C observer is greater than the total Proper-time elapsed for the A-b-C observer.
We do this by showing that "the Interval between A and b" is less than "the Interval from A and B". And, symmetrically, "the Interval between C and b" is less than "the Interval from C and B".
Since the Interval between two events is an absolute quantity, all observers agree on its value. (So, it is preserved by a Lorentz transformation.)
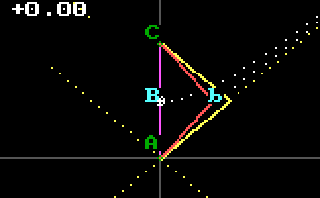The "Interval between A and b" is less than
the Interval between A and B".
(184 kb)
(19 kb)
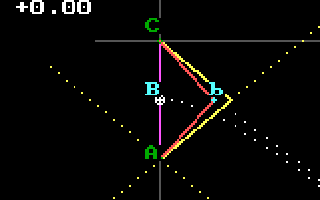The "Interval between C and b" is less than
the Interval between C and B".
(176 kb)
(18 kb)
Simply put:
A more illuminating look at the Light Cone
| Home |
|
PREFACE | PRIMEVAL | SPECIAL | GENERAL | CONCLUSION |
| Dictionary | Maxwell | Minkowski | Twins | Light Cone |