Home PREFACE PRIMEVAL SPECIAL GENERAL CONCLUSION
Dictionary Maxwell Minkowski Twins Light Cone

Maxwell and the Electrodynamic Theory of Light

Maxwell's Electrodynamics

James C. Maxwell
(1831-1879)
completed and unified
the theories of electricity and of magnetism
set down by
Carl F. Gauss
(1777-1855)		 Andre M. Ampere
(1775-1836)		 Michael Faraday
(1791-1867)

If you have a VRML-enabled browser, you can view some laws of electromagnetism as virtual worlds: VRML Gallery of Electromagnetism.
Although the laws of electricity and of magnetism according to Gauss, Ampere, and Faraday worked remarkably well, there was a glaring problem: taken together, these laws did not "conserve charge". In other words, for these laws (as written) to work, one had to allow charge to be created or destroyed. And this is not a good thing. (Additionally, from the form of the equations of these theories, he noticed an interesting symmetry (a similarity) in the way the electric field and the magenetic field appeared. It wasn't a perfect symmetry, however.)

Maxwell modified Ampere's Law by adding a single term to it. This was what was needed to make the laws consistent with the conservation of charge. (It also made the above symmetry closer to being a perfect symmetry.)

However, the addition of this term led to a remarkable prediction: the existence of electromagnetic waves. With the full set of equations, Maxwell was able to calculate the speed of these waves. He found that their speed was a constant, independent of the nature of the electric and magnetic fields. What Maxwell found was that electromagnetic waves traveled at the speed of light. Maxwell had just discovered a fundamental constant of nature: the speed of light. It just "popped out" of the full set of equations.

Thus, the Maxwell equations not only unify the theories of electricity and of magnetism, but of optics as well. In other words, electricity, magnetism, and light could all be understood as aspects of a single object: the electromagnetic field. Quite a remarkable achievement!

As a consequence, the Maxwell equations made the physical prediction that "light travels with the same speed, in all directions". In other words, "a spherical pulse of light will appear spherical".

But there's a problem....

Galileo's Relativity and Newton's Mechanics
(GALILEO'S SPACETIME)

vs.

Maxwell's Electrodynamics

Recall that Galileo's Principle of Relativity says that the mechanical laws of physics are the same for every inertial observer. And this led to the understanding that there is no public notion of speed---no universal agreement on what the speed of an object is---the speed of an object is a private "relative" concept. This is what led us to abandon Aristotle's notion of absolute rest and replace his spacetime with Galileo's Spacetime.

However, there is a serious problem: Galileo's Spacetime is incompatible with Maxwell's Laws of Electrodynamics and Optics. The source of the problem is the appearance of a "constant speed"--a fundamental constant of nature: the speed of light--automatically built into the Laws of Electromagnetism and Optics. (It turns out that if this speed were infinite, then there would be no conflict between Galileo's Spacetime and Maxwell's Laws of Electromagnetism and Optics. But, this speed is not infinite. So, there is a conflict.)


Here, we show that in Galileo's Spacetime, the speed of light (indicated by the slant of the diagonal yellow lines)

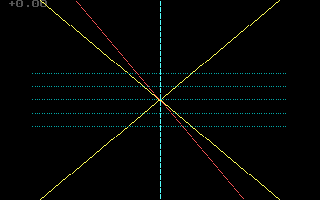
has a different value (since the slant of those lines have changed) in different directions, according another observer.


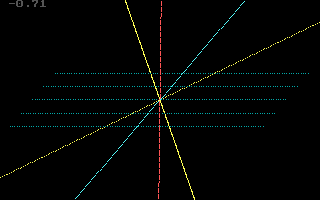
In this example, the red observer would say that the speed of "light traveling to the right" is less than the speed of "light traveling to the left".

Thus, the speed of light cannot be a constant for all inertial observers in Galileo's Spacetime.

Thus, Maxwell's Electrodynamics is incompatible with
Galileo's Spacetime.

There is a conflict.

Home PREFACE PRIMEVAL SPECIAL GENERAL CONCLUSION
Dictionary Maxwell Minkowski Twins Light Cone