Home PREFACE PRIMEVAL SPECIAL GENERAL CONCLUSION
Dictionary Maxwell Minkowski Twins Light Cone

The Einstein-Minkowski Spacetime:
Introducing the Light Cone

The Einstein Principle of Relativity

A. Einstein
(1879-1955)

In 1905, Albert Einstein published "On the Electrodynamics of Moving Bodies".

In it, he emphasized the physical experimental fact that electromagnetic phenomena do not appear to be dependent on the absolute motion of the laboratory, but just on the relative motion of the various components in the experiment. In other words, it appears that "by performing electromagnetic experiments, you cannot distinguish between absolute rest and uniform motion."

However, the Maxwell Laws of Electromagnetism (which is asserted to be correct) requires that the speed of light be the same constant, c, for every inertial observer. But this (as we have seen) cannot be maintained in Galileo's Spacetime.

Einstein realized this inconsistency and could have chosen either:

Recall that Galileo's Spacetime embodies Galileo's Principle of Relativity and Newton's Mechanical Laws of Motion. To give up Galileo's Spacetime would mean that there was something wrong with Galileo's Relativity or with Newton's Mechanics or with both.

Einstein felt so strongly about Galileo's Principle of Relativity (which applied to the mechanical laws) that he extended it to include electromagnetic and optical laws.

THE EINSTEIN
PRINCIPLE OF RELATIVITY

"ALL OF THE LAWS OF PHYSICS
are the same for every inertial observer."

In particular,

"The speed of light is the SAME for all inertial observers,
regardless of the motion of the source."

In other words, "no physical experiment (mechanical, electromagnetic, optical---or any physical law whatsoever) can distinguish between a state of absolute rest and a state of constant velocity."

With the help of the mathematician Herman Minkowski (who gave us the idea to think in terms of "Spacetime", not just space and time separately), Einstein proposed a new model for Spacetime to replace Galileo's Spacetime.

H. Minkowski
(1849-1909)
"Henceforth, space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality."

The Einstein-Minkowski Spacetime

The characteristic feature of Galileo's Spacetime was the set of horizontal slices representing "planes of simultaneity". On a given plane, all of its events are simultaneous. This is the notion of Absolute Time, in which all observers agree on the elapsed-time between two given events. In the particular case of "zero elapsed-time", all observers agree that the events on a given horizontal plane are simultaneous.

Einstein's extension of the Principle of Relativity to all physical laws requires us to abandon Galileo's Spacetime---in particular, its universal "planes of simultaneity"---that is, the notion of Absolute Time.

In its place, we have the Einstein-Minkowski Spacetime.

Introducing The Light Cone

The characteristic feature of this spacetime is the Light Cone, a double-cone centered at each event in Spacetime. (By the conventional choice of units used in relativity, the sides of the cone are sloped at 45 degrees. This corresponds to choosing units where time is measured in seconds and distances in light-seconds. A light-second is the distance light travels in one second.)

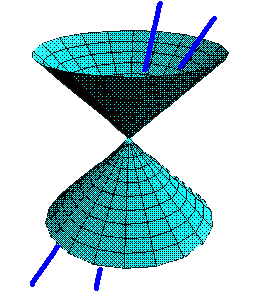
The Light Cone represents the idea that "the direction of the light-flash does not depend on the motion of the source---but just on the event at which the light-flash is emitted." In addition, by the Einstein Principle of Relativity, all observers, regardless of their motions, must (because of Maxwell's Laws) measure the speed of light to be the same constant, in all directions. That is to say, "all observers will universally agree on the Light Cones at each event." This means that each observer drawing a spacetime diagram in which he is at rest must have the worldlines of light-flashes at the same angle of 45 degrees from his worldline (his time axis), and 45 degrees from his plane of simultaneity (his space axes)."

The following animation will show how the blue line, which is slanted to the right in this diagram, becomes a vertical line, without altering the Light Cone. This operation is called a Lorentz transformation (named after the H.A. Lorentz, who first discovered the transformation but not its correct interpretation).

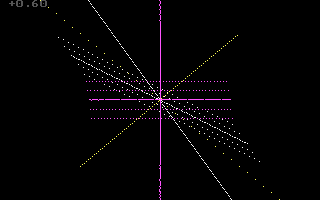A Lorentz Transformation
(1096 kb)
(11 kb)

The Fall of Absolute Time

Einstein immediately realized that a consequence of his postulate was that the our understanding of the nature of time needed to be revised. The set of events that are simultaneous to one observer are not simultaneous to another observer!

As an example, Einstein provided us the following "thought experiment" to show that "Simultaneity is relative".

Simultaneity is Relative:
A trip on Einstein's Train

Lightning strikes the front and back ends of a moving train. The lightning strikes leave marks on the train and on the tracks. Consider two observers:
Stan receives ("sees") the light emitted from events F and B simultaneously, and concludes that: "since I am midway between the marks on the tracks, and since the speed of light is a constant, then events F and B are simultaneous."

Mo receives ("sees") the light emitted from event F, then from B, and concludes that: "since I am midway between the marks on the train, and since the speed of light is a constant, then events F and B are NOT simultaneous: F occurred before B."

based on Taylor/Wheeler Spacetime Physics

Thus, each inertial observer will have a different sense of which events are simultaneous.

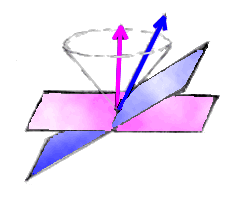
In the above diagram, the pink line represents one inertial observer, and he will regard events on the pink plane as simultaneous with each other. Similarly, the blue-line observer will regard events on the blue-plane as simultaneous with each other. Clearly, the two planes are different, and therefore they disagree on which events are simultaneous. Simultaneity has become a relative, observer-dependent concept.

(Note: In the diagram, the blue plane is spacetime-perpendicular (though "not Euclidean-perpendicular", that is, "not perpendicular in the usual sense") to the blue worldline.)

In Einstein-Minkowski spacetime, each observer will slice up spacetime in his own way. There is no universal way to slice it up.

Einsteinian Map Reading 301:
How to recover "space" and "time" from "spacetime"

How does one recover the notions of space and time from this spacetime?
As Minkowski suggested in his quotation, and as we've been doing all along, space and time are shadows of spacetime. In this case, each observer will project shadows of events onto his own worldline (his time axis) and his own plane of simultaneity (his space axes).

How do we know what those planes are?
Planes refer to events that are not on our worldline. They are at a distance (i.e., spatially separated) from us.

How does one make measurements of distant things?
Metersticks won't work: Why?

  • although the length of "a meterstick at rest" could make sense, who's to say who is at rest?
  • although the length of "a moving meterstick" makes sense if the ends are measured simultaneously (with two events), who's to say that those two events are simultaneous?

Use RADAR!
Equip each observer with a wristwatch and a flashlight.

  • We send out a light-flash, aimed at just the right direction and emitted at just the right time, so that signal hits the event of interest.
  • and then, wait for its echo.
    In other words, use the Light Cone of the event of interest.
  • By making three time-measurements (by looking at my wristwatch), we can determine the "spatial distance" and "time elapsed" between that distant event and some event on my worldline.

I won't explain the details here. They will appear later, if you are interested in them.

For now, let us just do an important example:

Example: Finding my plane of simultaneity

Given an event O on my worldline, find my plane of simultaneity.

Set my wristwatch to read 12:00 at event O.
Suppose I sent out a light-pulse at 11:59, suitably aimed so that the pulse will reach event X.
And suppose I receive an echo from event X at 12:01.

What could I say about event X?

  • Well, it took two minutes to get there to event X and back. So, it must have taken light one minute (that is, half the roundtrip-time) to get to X.
  • Well, if it was there one minute after I sent the light-pulse out, my watch must have read 12:00 when the pulse reached X. Therefore, I say that "event X is simultaneous with event O."
  • And, since the light-pulse, travelling at the speed of light, took one minute to get to X, then I say that "event X is a length 1 light-minute away from event O." (This length makes sense to me because I measured it between two simultaneous events.)
Suppose I had sent out another light pulse earlier at 11:58 toward event Y and received its echo at 12:02. I would say "event Y is also simultaneous with event O, and it is 2 light-minutes away from me." ...and, so forth.

I would say that all such events would be simultaneous with event O.

Realize, however, that MY determination of "which events were simultaneous with event O" will generally differ from that of another observer (even if event O is also on his worldline).

Einstein's big lesson is that
SIMULTANEITY IS RELATIVE.

Is there anything absolute (universal)? It seems as if we've gotten rid of everything that has to do with universal notions of time and universal notions of space. Our spacetime model can no longer have these once-universally accepted lines and planes. What The Principle of Relativity has done is to make the Light Cone absolute.

It is fair to say that what Einstein did is that he replaced the absoluteness of time and of space with the absoluteness of light. Light is more fundamental than time and space.

This is such a radical departure from common sense that people (physicists, philosophers, you and I) have been struggling to make sense of it. Realize that it's more than just a matter of taste here. Einstein's theory makes physical predictions (which differ markedly from the physics of Newton). And these predictions have been experimentally tested and verified. As far as we can tell, in the domain of its applicability, Einstein's Theory of Relativity is correct.

Here is one example of a supposed paradox of the Theory of Relativity.
The Twin Non-Paradox
Home PREFACE PRIMEVAL SPECIAL GENERAL CONCLUSION
Dictionary Maxwell Minkowski Twins Light Cone
Rob Salgado
27-Nov-1995