A more illuminating look at
The Light Cone
Last updated 15 Jun 1996.
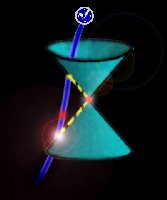
click to see this Light Cone rendered in VRML
|
|---|
The Light Cone
(1905-present) |
Recall that the future Light Cone of an event is
the future-history of a light-flash of emitted at that event.
It is an absolute surface for the Einstein-Minkowski Spacetime.
The Light Cone plays additional roles in Einstein's Theory of Relativity:
The fact that the speed of light is finite
(that is, not infinite)
is crucial to the Light Cone.
At the end of this page, we
consider the "Galilean limit",
in which we pretend that "the speed of light is infinite".
In doing so, we can understand why our common sense intuition is
"Galilean" and not "Einsteinian".
Causal Structure
Causal structure provides each event
in spacetime with its own notion of ordering events
into "those events to its past", "those events in
its present", and "those events to its future".
Given an event
- events to its past could have influenced it
- events to its future could be influenced by it
An example
As an example, consider again the trip on Einstein's Train.
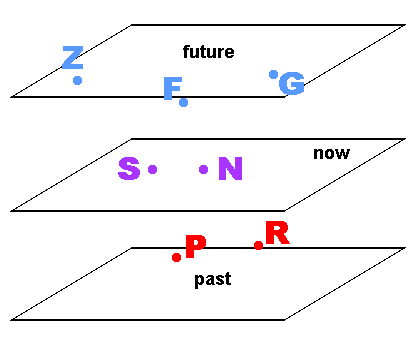
Aristotle's Spacetime and Galileo's Spacetime
In Aristotle's Spacetime and Galileo's Spacetime,
their absolute "horizontal planes of simultaneity"
defined the following causal structure:
For a given event, consider the particular the absolute hoizontal plane
on which this event sits.
Events lying above this plane (in the diagram) are
"events to the future" of our given event.
Events lying below this plane (in the diagram) are
"events to the past" of our given event.
Events lying at the boundary between future and past
(that is, on its horizontal plane) are "events happening now"
(that is, "simultaneous").
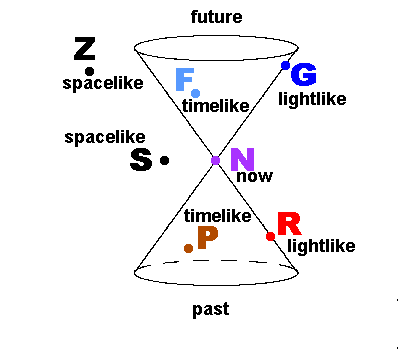
Einstein-Minkowski Spacetime
In Einstein-Minkowski spacetime, the causal structure is different.
The Light Cone at that event divides spacetime into distinct regions:
causal-future, causal-past and spacelike.
Causal can be further divided into timelike and lightlike.
The Ultimate Speed Limit
The Light Cone places an upper speed limit for all objects.
Only "massless" particles can travel along the cone. For example,
a photon ("a particle of light") is massless.
Thus, our worldlines are confined to always be within the Light Cone.
Measurement
For the interested reader, we give the details of measurement of time and space
using the "RADAR method".
Equip each observer with a wristwatch and a flashlight.
- We send out a light-flash, aimed at just the right direction and emitted
at just the right time, so that signal hits the event of interest.
- and then, wait for its echo.
In other words, use the Light Cone of the event of interest.
- By making three time-measurements (by looking at my wristwatch),
we can determine the "spatial distance" and "time elapsed"
between that distant event and some event on my worldline.
Here is a spacetime diagram of a RADAR measurement:
- "Ref" is an event "on my worldline, my wristwatch reads tref".
- "X" is the event I am interested in.
- "Send" is the event "my wristwatch reads tsend
when I emit the light-pulse"
- "Echo" is the event "my wristwatch reads techo
when I receive the echo of my light-pulse"
Define
- t1=(tref-tsend), "the elapsed-time between your Sending the pulse and
your Reference event".
- t1 < 0, if "you send after your reference event".
- t1 = 0, if "you send at your reference event".
- t1 > 0, if "you send before your reference event".
- t2=(techo-tref), "the elapsed-time between your reference event
and your receiving the echo."
- t2 < 0, if "you receive the echo before your
reference event".
- t2 = 0, if "you receive the echo at
your reference event".
- t2 > 0, if "you receive the echo after
your reference event".
Interpretation of the order of operations:
- "reference, send, echo" means that t1 < 0
and t2 > 0, so t1t2 < 0
- "reference=send, echo" means that t1 = 0
and t2 > 0, so t1t2 = 0
- "send, reference, echo" means that t1 > 0
and t2 > 0, so t1t2 > 0
- "send, reference=echo" means that t1 > 0
and t2 = 0, so t1t2 = 0
- "send, echo, reference" means that t1 > 0
and t2 < 0, so t1t2 < 0
- "send=reference=echo" means that t1 = 0
and t2 = 0, so t1t2 = 0
Spatial separation:
spatial separation =
(1/2)ctroundtrip = (1/2)c(t1 + t2)
Elapsed time:
elapsed time = (1/2)(t2-t1)
The Galilean Limit
Recall that the convention in relativity is to draw
a spacetime diagram in which the Light Cone
appears with the sides slanted at 45 degrees away from the vertical.
This has the effect of setting the relative scales between "time"
and "space" measurements: 1 second, 1 light-second.
However, realize that 1 light-second is a huge distance: 300,000 km
(186,000 miles). It is instructive to draw a spacetime diagram
using a more practical common-sense scale. Where is the Light Cone?
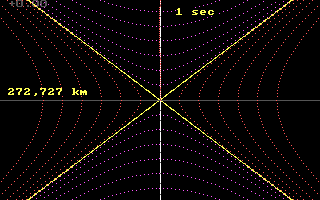
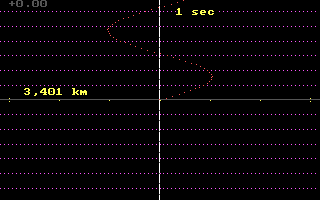The Galilean Limit
(912 kb)
(53 kb)
On a common-sense scale, the Light Cone "practically coincides" with
our personal plane of simultaneity. In fact, the personal planes
of simultaneity of other people near us also "practically coincide".
In other words, our daily experiences expose us to only a small
part of our Light Cone... and thus, spacetime looks like Galileo's Spacetime
to us.
This explains why we have a "Galilean" intuition about the
nature of time. If, someday, we are able to experience
high-speeds near the speed of light, we will develop a common-sense
intuition for Einstein's Theory of Relativity.
Rob Salgado
15-Jun-1996
(53 kb)